These pressurisations are needed to ensure that the bomb has had all the air (and moisture) removed from the bomb and be replaced by an excess of oxygen. The oxygen is required to ensure complete combustion of a sample.
2. The bomb calorimeter
2.1 The operation of the calorimeter
A bomb calorimeter (diagram 1) works by the ignition of a sample in an excess of oxygen. This is achieved by pressurising a number of times up to 25 atmospheres. These pressurisations are needed to ensure that the bomb has had all the air (and moisture) removed from the bomb and be replaced by an excess of oxygen. The oxygen is required to ensure complete combustion of a sample.
The ignition is initiated by passing a large voltage across a bare fuse wire which has been suitably fixed into the sample. This fixing is normally performed by tying one end of a known mass (and length) of cotton around the fuse and then the other end around the sample (see diagram 2). The voltage shorts out the fuse which triggers the reaction. The heat given out by this process is the energy of combustion for the substance.
Diagram 2 shows how the bomb is set internally. It can be clearly seen that the system is prone to errors by either fuse wire breaking or the cotton coming adrift with the increase of gas pressure on pressurisation.
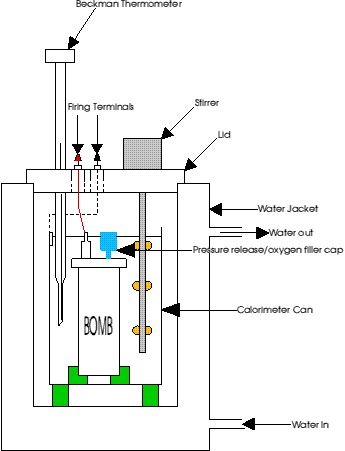
Diagram 1. A typical bomb
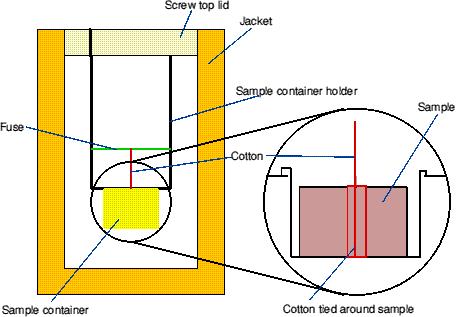
Diagram 2 - Internal representation of the steel bomb calorimeter calorimeter
The actual heat of formation is the change in heat content when one mole of compound is formed from its constituent elements in their standard physical states at 298.15K and 1 atmosphere pressure.
2.2 Calorimeter calibration
In order to correct for heat losses in the system, it is necessary to calibrate the calorimeter to find the energy equivalent of the calorimeter (how much energy the calorimeter will absorb during the process). This is denoted by e.
The bomb calibration is performed by the ignition of a known mass of a standard substance under 25 atmospheres of oxygen. There is a rise in temperature of the surrounding water which is measured. The calorimeter is a constant volume reaction vessel and thus the temperature rise is related to the energy of combustion from which the enthalpy of combustion is derived. The quantities are related in the following equation.
where †E is the total energy of combustion, e is the calibration constant and †T the temperature rise.
It is normal to use AR grade benzoic acid for calibration. This is of very high purity and so the enthalpy of combustion is known to a high degree of accuracy.
2.3 Calorimeter design and mathematics
The design of the calorimeter is of great importance. It should be so made that there are negligible losses of heat to the surroundings. These losses are important: to obtain a reasonable result, an accurate estimate of the energy of combustion is required. When the temperature difference between the calorimeter and surroundings is small, the heat exchange (due to both radiation and convection) is directly proportional to the temperature difference (Newton's Law).
These changes can be monitored by the use of a temperature vs. time plot (diagram 3).
Diagram 3. Temperature vs. time graph.
The calorimeter is set at a temperature a few degrees below that of the jacket (Tj). This is so that the final temperature will be very close to that of Tj. The true temperature rise, †T, due to the combustion may be calculated.
The time scale is split into three distinct sections; fore, during and after reaction. The substance is ignited at the end of the fore period. There is a time - lag between the ignition and the heat being transmitted to the calorimetric fluid (water). The after period begins when the graph has become linear again. The reason for recording these fore and after periods is to enable an accurate correction for the heat gained from the environment during the reaction period.
By Newton's Law,
where K is a constant and z is the leakage modulus correction constant (for constant sources of heat production or loss such as stirring or evaporation).
The average rates of temperature change, R (from Newton's Law) for each of the periods can be denoted thus:
where T (for each part of the reaction) is the mean temperature for the period. K is derived by the subtraction of (5) from (3) to give
Tj and z are removed from (4) by the subtraction of (4) from (5)
From here, the temperature rise, †T, is given by
Since the fore and after periods are assumed to be straight lines,
The average temperatures are:
The average temperature during the reaction period is calculated using a numerical integration procedure using (13)
This type of calculation is best performed by computer. There are a large number of programs available to do this.
An alternative to using the computer to calculate the area under the curve, is to use the Simpson Rule. The Simpson Rule is expressed as follows:
where h equals the difference between each reading (for example, a minute), F is the first reading, L is the last with E and O being the even and odd readings respectively.
This has the obvious advantage of being able to calculate the area on the same spreadsheet (or in the lab) without all the tedium of integrating values and subsequent calculations. It does have the disadvantage of being an approximation, but the level of error will be small (if enough readings are taken).
The type of bomb used for the initial parts of the work was the steel type, however, a test method was still required for the chemical of interest, nitrogen triiodide.
2.4 The glass bomb calorimeter.
2.4.1 Description and operation
A different type of bomb was required for the direct measurement of the triiodide to ensure the results from the first type of bomb were in the correct region. The results produced from the steel bomb were not reproducable to a high enough degree of accuracy.
The steel calorimeter has a problem in that the results obtained vary by up to 15% from one run to another. The upshot of this is that the calorimeter only really gives an indication rather than an absolute value. The glass bomb gives reproducable results which vary with a maximum of 1%.
The second bomb was constructed at the University of Salford by myself, Ken Bullock and Dr. Judah Arotsky (diagram 4). I designed a new type of bomb which would be suitable for the testing of the solid. It met with the criteria of using a capsule which has a very low thermal capacity, was small enough not to require the 25 atmospheres pressure and above all, was versatile. The design of this is below.
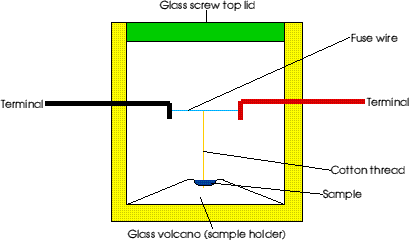
Diagram 4 - The glass bomb calorimeter
The measurement of heat given out was done in a polystyrene cup (the thermal capacity of this can be considered as zero) which also contained a glass bead thermistor. The thermistor is connected up to a PC and using a program written by Dr. Arotsky in Visual BASIC, monitor the temperature change over time. The container was filled with water and left to reach thermal equilibrium. Diagram 5 shows the set up.
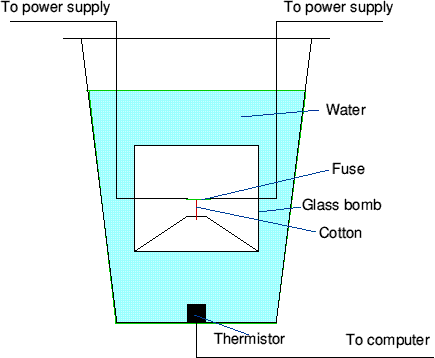
Diagram 5 - Set up for the glass bomb calorimeter
2.4.2 The pros and cons of the glass bomb calorimeter.
This type of bomb has a number of advantages over the conventional type of bomb. The advantages are as follows.
1. The experiments are far more convenient. This is because to the bomb does not require a circulating water bath. Also smaller amounts of sample are used (between 0.3 g and 0.7 g are all that are typically required for a result compared to around 1g for the conventional steel bomb calorimeter).
2. The experiment is far more accurate. The thermistor and computer system is able to read temperatures to four decimal places and is also able to take into account fluctuation of external factors. The computer can also deal with the standard deviation for the external temperature over time, thus reducing errors in the final analysis. While it is possible to adapt a conventional steel bomb calorimeter to use with a computer, the system is very complex since the thermistor needing to be embedded into the wall of the bomb.
3. The experiment is more reproducable. When the experiments were performed in the traditional type of bomb, the results obtained could be reproduced, but not to a very high degree of accuracy. The new bomb gave an accuracy of ±1% when tested again with the same sample or tested again with benzoic acid.
4. As the amount of water surrounding the bomb was not very great, the transfer of heat from the bomb to the thermistor will be fairly rapid. Though it would be better to have the thermistor above (or even in) the glass calorimeter, the practical implications would deem it unworkable. If the bead was embedded into the glass and the glass shattered, the bead would be destroyed. There would also be problems in inserting the calorimeter into the cup.
5. There are no dangerous pressures needed and so it is not covered by the Pressured Vessels regulations 1986[3]. The excess of oxygen is created by either placing the sample and bomb in an oxygen tent or high oxygen content area (such as in inflated glove bag) or having a constant current of oxygen passing through the bomb with the lid off. The method of constant oxygen movement introduces more errors than it eliminates (due to disruption of the sample in the sample holder and subsequent detonation).
The major drawback to this type of bomb is that it is made from Pyrex borosilicate glass (This has a constant composition and a known heat capacity. It is also relatively inexpensive and easy to obtain). However, any crack or scratch in the glass will mean that the bomb will fail on ignition, meaning a spoiled experiment.
To achieve as few as possible problems with the glass (such as excessive internal strains), the electrodes were sealed into the glass wall. The "volcano" structure was added as part of the bomb itself. This "volcano" also had the advantage of giving extra strength to the bomb and was somewhere for the sample to rest. The "volcano" is made out of glass and is solid.
A thermoset plastic has also been tried for the bomb, but the thermal capacity altered over time and so after every five or six tests, the bomb needed re-calibrating. The accuracy for duplicate testing was also lower than that for the glass at ± 5.75%. The structure was exactly the same.
[3] Health and Safety Executive - Pressure Vessel Regulations, 1986